Now that you understand what equilibria are (and if you don’t, check this out), it’s time to start doing some math.  For those of you who aren’t big fans of math, don’t worry – it’s not as bad as it sounds.

Get a grip, dude.

Before we get started, it’s time to go back to our friend from the kinetics tutorials, the rate constant.  As you’ll recall, the rate constant is a value called “k” that allows us to figure out the relationship between concentration and reaction rate.  For a reaction with the general format A + B → C + D, the rate of the reaction can be expressed as:

rate = k[A]ˣ[B]ʸ

Where “x” is the order of the reaction in A and “y” is the order of the reaction in B.  If you don’t know what all this means, think back to the kinetics stuff that you learned a while back.

In any case, equilibrium processes have forward and reverse rates that are the same.  Or, in math terms:

rate(forward) = rate(reverse)

Given that there are two reactions, one in which A + B → C + D and the other where C + D → A + B, we end up with two rate expressions.  Namely:

Where “z” is the order of the reaction in C and “n” is the order of the reaction in D.  “kf” and “kr” refer to the rate constants of the forward and reverse reactions, respectively, while “ratef” and “rater” equal to the rate of the reaction in the forward and reverse directions.

At equilibrium, we run into a cool situation where the forward and reverse rate of the reaction are the same.  This allows us to come up with a single expression to relate the equilibrium to the concentrations of every chemical involved:

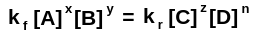
Using the power of algebra, we can just go ahead and, for what seems like no reason at all, separate some of the terms from each other.  Not to worry, there’s a reason for doing this:

And, given that both “k” terms are constants (they are, after all, called “rate constants”), we can just combine them together in a term we’ll call the equilibrium constant:

This, my friends, is the equation that we use to do math using equilibria.

---

An aside:  Figuring out z, n, x, and y

You may be wondering, given the complexity of rate laws, how you can figure out the z, n, x, and y superscripts in this equation.  For complicated reactions, this can be very difficult, but for chemistry that you’re likely to run into, just use the coefficients in front of each compound in the equation to figure it out.  For example, in the case of the reaction:

The equilibrium expression would be:

Where the superscript over nitrogen is 1 because there’s no number in front of it in the equation, the superscript in front of water is 2 because there’s a 2 in front of it in the equation, and so forth.

---

How can we use this expression?

Well, let’s say that the following chemical reaction takes place with the following rate law:

Now, let’s say that the equilibrium constant for this reaction is 3.6 x 10⁻¹¹ for this process.  Given all this cool info, here’s a practice problem:

Example:  I have a solution that contains 0.50 M of compound A and 0.20 M of compound B.  If I start with no C at all and let the reaction run for a while, what will the equilibrium concentrations of each compound be?

Answer:  Plug it all into the equilibrium expression.

Here’s how:

• Initially, you’ve got 0.50 M of compound A.  At equilibrium, some of it will have reacted to form C.  How much?  We don’t know, so let’s just say that the concentration has decreased by “x”.  This means that at equilibrium, the concentration of A will be “0.50 – x” M.
• Initially, you’ve got 0.20 M of compound B.  At equilibrium, some of it will have reacted to form C.  Again, the concentration has decreased by “x”, which means that the equilibrium concentration will be “0.20 – x” M.
• Initially, there’s no C at all.  However, when A and B react, some unknown quantity of C will form.  We don’t know how much this is, but we do know from the chemical equation that the amount that forms will be twice as much as the amount of A and B that reacted.  Our equilibrium concentration, then, will be 2x M.

From here, it’s a simple matter of plugging all of these values into the expression for the equilibrium constant to figure out what this mystery x value is:

And, using our friend the quadratic equation, we find that x = 0.0043, which means that:

[A] = 0.50 – 0.0043 = ~0.50 M

[B] = 0.20 – 0.0043 = ~0.20 M

[C] = 2(0.0043)² = 3.7 x 10⁻⁵ M

Wasn’t that fun?

---

No.  It was not fun.

Most of us don’t like using the quadratic equation much.  It’s kind of annoying to memorize and anybody with any sense just goes online to find something that will calculate it for you (here’s where I did it).  Not fun.

However, let’s consider this:  In many equilibria, the amount of product that’s formed isn’t very much.  As a result, we can assume that “x” is going to be much smaller than the concentrations of the reagents we started with.  What this means is that the term [0.50 – x] can just be written as [0.50], since subtracting a very tiny number from 0.50 still gives you basically 0.50.  Using this simplification, we can simplify the equation above to give us:

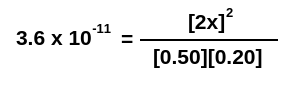
Which, when solved, gives us an x value of 0.0042 M.  This isn’t identical to what we found above, but it’s a pretty small difference.  Most of the time, that’s A-OK with us.

---

Image credits: 

Screaming guy:  Image courtesy of imagerymajestic at FreeDigitalPhotos.net